گروه ریاضی متوسطه استان لرستان
نمونه سوال-بارم دروس-طرح درس-بخش نامه ها -همایشها-المپیادهاگروه ریاضی متوسطه استان لرستان
نمونه سوال-بارم دروس-طرح درس-بخش نامه ها -همایشها-المپیادهامقاله ریاضی وهنر نوشته زینب دادور دبیر ریاضی ناحیه دو خرم آباد
چکیده
آنچه در این مقاله بیان می شود برداشتی از بررسی و مقایسه هنر و ریاضی است.
هر پدیده زیبا در طبیعت می تواند از دو نظر مورد توجه قرار بگیرد، هم از نگاه هنری وهم از دید ریاضی ونظم منطقی .هنر و ریاضی همانند یکدیگرند، زیرا در هردو مفاهیم تناسب ، تقارن و توازن نقش مهمی دارند.
هنرمندان معمولاً محدوده و فضای اثر هنری خود را از یک طرح ریاضی انتخاب می کنند .به طور کلی ترسیم هر شکل نیازمند بعضی ترسیمات کمکی است که به وسیله آنها نقاط ، خطوط ویا سطوح آن شکل تعریف می گردد.مفاهیم سطح و حجم چه در ریاضی و چه در هنر بسیار مورد استفاده قرار می گیرند.
کاربرد تناسب ها به دلیل ایجاد زیبایی بصری در هنرهای تجسمی از اهمیت ویژه برخوردار است تقریباً همه آثار هنری بر اساس نوعی تناسب به وجود آمده اند .نقاشان و هنر مندان برای جان دادن به اشیاء و القای فضای سه بعدی به ریاضی روی آورده اند و می توان گفت هندسه نخستین نیاز یک نقاش است. در مجموع ایجاد ضابطه هندسی در ترکیب شکل ها ، نه تنها مقدار زیادی از عملیات ترسیم را کاهش می دهد بلکه باعث صرفه جویی در وقت خواهد شد.
مقدمه
انسان همواره با تلاش خستگی ناپذیر رو به سوی کمال خویش دارد، بیش از آنچه هست طلب می کند.عقاب خیا ل و اندیشه خویش را تا دورترین نقاط افلاک و کاینات به پرواز در می آورد ودل هر ذره را می شکافد تا به جهانی از نا شناخته ها دست یابد و جهان را زیر سیطره قدرت خویش کشد.و همچنان نا آرام و بی قرار از آنچه هست، ناراضی می ماند.
انسان، زمانی انسان شد که به کمک دستان خود، کارکردن با اشیا طبیعی را فرا گرفت و به ساختن ابزار پرداخت . انسان ابزار ساز با دست آفریده ی خویش ، موجودیتی نو یافت و راه به سوی تکامل گشود . در این مسیر تکامل فکری ، بشر موفق شد ،به جای استفاده از اشیا ء که در طبیعت مشابه آن ها یافت نمی شد . و این نشانی است از زایش قدرت آفرینندگی در ذهن انسان پیش از تاریخ ، و از این رو انسان دیگر برای برتری و استیلا بر طبیعت ، به نیروی نامحدودی دست یافت که هنر یکی از بارزترین و شکوه مند ترین جلوه های آن به شمار می رود . حال سؤال این است که آیا هنر به تنهایی کافی است که انسان بتواند از خود دست آفریده های هنری به یادگار بگذارد ؟
اگر این را بپذیریم که ، تصور و خیال ، یکی از سر چشمه های اصلی آفرینش های هنری است آن وقت ناچاریم قبول کنیم که در ریاضیات هم ، دست کم عنصر های زیبایی و هنر وجود دارد چرا که مایه ی اصلی کشف های ریاضی ، همان تصور و خیال است .
با هیچ نیرنگی ، نمی توان از کشش انسان ها به سمت زیبایی ها جلوگیری کرد و آن چه زشت و نا زیبا است را جانشین زیبایی ها کرد .
« رودن » مجسمه ساز مشهور فرانسوی می گوید : «من یک رویا پرداز نیستم بلکه یک ریاضی دان ام . مجسمه های من تنها به خاطر این خوب اند که ساخته و پرداخته ی اندیشه ی ریاضی اند . »
هر انسانی از تماشای چشم انداز یک دامنه ی سر سبز آرامش خود را با زمی یابد ، در عین حال به فکر فرو می رود . نقاش با قلم و بوم خود تلاش می کند که دیگران را در شادی خود شریک کند و ریاضی دان نحوه ی قرار گرفتن گل و گلبرگ ها یا اندازه و شکل ها را مورد مطالعه قرار می دهد . ولی هم گیاه عضوی یگانه است و هم انسان و اگر بخواهیم برخورد انسان با گیاه را بررسی کنیم ناچاریم ، به همه ی این جنبه ها توجه داشته باشیم .
ارتباط ریاضی با هنر
در دوران رنسانس ، نقاشان بزرگ ، ریاضی دانان هم بودند . آلبرتی نخستین نیاز نقاش را هندسه می دانست . او بود که در سال ۱۴۳۵ میلادی ، اولین کتاب را درباره پرسپکتیو نوشت . نقاشان و هنرمندان برای جان دادن به تصویر ها و القای فضای سه بعدی به آثار خود ، به ریاضیات روی آ ورند . بنابراین همه ی نقاشان دوره رنسانس نظیر آلبرتی ، دیودر ، لئوناردو داوینچی ، ریاضی دانان هنرمند یا هنرمندانی ریاضی دان بودند .
طبیعت ، سرچشمه زاینده و بی پایانی است برای انگیزه دادن به هنرمند و ریاضی دان . آن ها از درون خود و از ایده ها سود میجویند و حقیقت را نه تنها آن گونه که مشاهده می شود ، بلکه آن که باید باشد و آرزوی آدمی است ، می بینند . هنر و ریاضیات هر دو کمال و ایده ال را می جویند . در واقع تمامی عرصه ریاضیات سرشار از زیبایی و هنر است . زیبایی ریاضیات را می توان در شیوه بیان موضوع ، در طرز نوشتن و آرا یه آن در استدلال ها منطقی آن ، در رابطه آن بازندگی و واقعیت ، در سرگذشت پیدایش و تکامل آن و در خود موضوع ریاضیات مشاهده کرد یکی از راه های شناخت زیبایی های ریاضیات ( به خصوص هندسه ) آگاهی بر نحوه پیشرفت و تکامل است . جنبه دیگری از زیبایی ریاضیات این است که با همه انتزاعی بودن خود ، بر همه دانش ها حکومت می کند و جز قانون های آن ، هم چون ابزار نیرو مند دانش های طبیعی و اجتماعی را صیقل می دهد ، به پیش می برد . تفسیر می کند ودر خدمت انسان قرار می دهد .
ریاضی دان انگلیسی«ج.ه.هاردی » معتقد است :
معیار ریاضی دان مانند معیار نقاش یا شاعر ،زیبایی است . اندیشه ها هم مانند رنگها یا وا ژه هاباید در هماهنگی کامل و سازگار با یکدیگر باشند . زیبایی نخستین معیار سنجش است .
همیلتون ریاضی دان ایرلندی در یکی از سخنرانی های خود در ارتباط با نجوم گفته است : «هنر و ریاضیات همانند یک دیگرند ، زیرا در هر دو مفاهیم تناسب ، تقارن و توازن نقش مهمی دارند . »
انیشتین می گوید : « تخیل مهم تر از معلومات است » که منظور تخیلات واهی نیست بلکه تفکر و ادیشه در مسائل و مفاهیم علمی است که باعث خلاقیت می شود .
به قول شاعر که می گوید :
« میاسای از اندیشه گونگون
که دانش ز اندیشه گردد فزون »
هر چیز که در طبیعت زیبا جلوه کند می توان هم به دید ریاضی و هم به دید هنر به آن نگاه کرد و از طرفی می توان ملاحظه کرد که ریاضی هم می تواند به صورت یک هنر جلوه کند. یک اثبات زیبا برای یک مسئله یا قضیه ی ریاضی ازدید یک ریاضی دان یک هنر است پس با کمی دقت ملاحظه میشود که هنر وریاضی کاملا″ قابل مقایسه می باشند که ریاضی یک هنر بدیع وهنر قابل بیان به زبان ریاضی است.
در این جا لازم است به نکته ای توجه کنیم که گاهی عواطف انسانی در جلوه ی زیبایی تاثیر گذار باشد این تفکر ایجاد شود که حتی مثال نقضی برای تعریف هنر باشد در صورتی که چنین نیست و همان طور که در تعریف هنر از دید هنرشناسان بیان شده لزوما″معیارهای زیبایی ازدیدگاه های مختلف ممکن است یکی نباشد ولی با تعریف کلی مطابقت دارد.همچنین افرادی در یک هنر تخصص نداشته باشند زیبایی آن هنر برای این افراد قابل درک نیست . به عنوان مثال زیبایی که یک هنرمند نقاش در تابلوی معروف لبخند ژوکوند اثر لئوناردوداوینچی می بیند برای کسی که با هنر نقاشی و سبک این نقاشی آشنا نباشد متفاوت است . در همین رابطه و جلوه های زیبایی ریاضی می توان به اثبات آخرین قضیه ی فرما اشاره کرد که توسط اندره وایلد و شمورا انجام شد که یک شاهکار هنری قرن بیستم برای ریاضی دانان می باشد پس ملاحظه می شود که هنر و ریاضیات در مفهوم کلی کاملا″ قابل مقایسه اند.
کادر یا قاب تصویر محدوده ی فضا یا سطحی است که اثر تجسمی در آن ساخته می شود . به طور کلی منظور از کادر در هنرهایی که با سطح سر و کار دارند و بر سطح به وجود می آیند همان محدودهای است که هنرمند برای ارائه و اجرای اثر خود بر می گزینند .
کادر می تواند اندازه ها و شکل های گونا گونی داشته باشد مثل انواع چهار گوش با ابعاد و تناسبات مختلف به صورت مربع و مستطیل های متنوع عمودی و افقی .هم چنین شکل های دیگر هندسی مثل دایره ، بیضی ، مثلث یا حتی تلفیقی از این اشکال به صورت منظم و غیر منظم به کار عنوان کادر به گرفته می شوند .
هنر مندان معمولا″ ترکیب عناصر و نیرو های بصری کار خود را براساس کادر و فضای بصری ، که در اختیار دارند ، سازماندهی می کنند محدوده و فضای اثر هنری به هر شکل که انتخاب شود در تأثیر گذاری بر نیرو های بصری و ترکیب آن ها با یک دیگر مؤثر است . کادر های هندسی مثل انواع چهار گوش ، سه گوش و دایره محدوده ای هستند که اثر تجسمی در آن ها به وجود می آید .
نقطه از دیدگاه ریاضی ، عنصری است که هیچ گونه بعدی ندارد ، فضایی را اشغال نمی کند ، در ابتدا و انتهای هر خط قرار دارد و بالاخره از تقاطع و تماس دو خط به وجود می آید و نقطه موضوعی ذهنی است که در فضا یا بر صفحه تصور می شود ، بدون این که قابل دیدن و لمس شدن باشد . اما این مفهوم ذهنی وقتی بخواهد نشان داده شود با استفاده از یک ابزار اثر گذار مشخص می شود که در این صورت تبدیل به یک نقطه بصری خواهد شد . مثل نشان دادن مرکز یک دایره یا محل تقاطع دو پاره خط ، یا وقتی بخواهیم خطی را بر صفحه ای ترسیم کنیم اولین تماس ابزار ما با صفحه یک نقطه خواهد بود .
خط
خط از دید گاه ریاضی از به هم پیوستن نقطه ها به وجود می آید دارا ی طول اما فاقد عرض است ، نشان دهنده جهت و موقعیت است . و مرز سطح را شکل می دهد و آن را محدود می کند . خط عنصر اصلی طراحی است که در جریان آفرینش هنرهای تجسمی نقشی اساسی را ایفا می کند . خط اغلب بیان کننده عواطف واحساسات و نشانگر تفکر و اندیشه و آرمان های ذهنی هنرمند است .
خط به عنوان وسیله ی اصلی طراحی برای نمایش دادن ،شکل، ایجاد تیرگی وحجم نمایی به کار می رود.
یک طراحی معمولا″در مرحله ای دیگر برای ساختن نقاشی استفاده می شود.
سطح
شکلی که دارای دو بعد باشد سطح نامیده می شود. همچنین روی چیزها را نیز سطح می گویند. همه ی سطح ها از سه شکل هندسی دایره ، مربع ، مثلث یا ترکیبی از آنها به وجود می آیند .
دایره شکل کاملی است که حرکت جاودانه و مداومی را نشان می دهد ،آسمان بلند که شعرا به آن دایره مینایی می گویند همه و همه نشان دهنده تناسبی است که میان شکل دایره و اشکال متنوع طبیعت وجود دارد بسیاری از هنر مندان به ویژه در هنر ایرانی نقاشان بزرگ برای ساختن آثار خود از ترکیبهایی بر اساس دایره و چرخشی الهام گرفته اند.
مربع یکی دیگر از شکل های پایه و ساده ی هندسی است ، از تغییرات زاویه ها و ضلع های مربع اشکال چهار گوش متنوعی به وجود می آید این شکل مظهر قدرت زمین و مادی و در عین حال اززیباترین اشکال هندسی است و نماد صلابت ، استحکام و سکون است.
مثلث متساوی الاضلاع نیز دارای سه ضلع و سه زاویه مساوی است هنگامی که این شکل بر سطح قاعده اش قرار بگیرد پایدارترین شکل هندسی است و مثل یک کوه استوار به نظر می رسد.مثلث به واسطه زوایای تندی که دارد سطحی مهاجم و شکلی ستیزنده به نظر می رسد که همواره در حال تحول و پویایی است .استفاده از مثلث و شبکه های مثلثی یک اصل ساختاری در طبیعت به شمار می رود.
از تکرار و ترکیب شکل های مثلث ، مربع و دایره می توان سطح های متعدد منظم و غیر منظمی به دست آورد همچنان اگر ا شکال پیچیده و آلی طبیعت را تجزیه و ساده کنیم مجدداً به ا شکال ساده دایره، مثلث و مربع خواهیم رسید .
حجم
به چیزهایی که دارای سه بعد : طول و عرض و ارتفاع یا عمق باشند حجم گفته می شود معمولاً همه اشیاء مادی در طبیعت ،
دارای حجم هستند .این حجم ها گاهی به طور طبیعی به صورت نسبتاً منظمی دیده می شوند . مثل حجم برخی از درختها ،
میوه ها و تخم پرند گان و جانوران ، اما بیشتر اوقات به شکل غیر منظم جلوه می کنند ، مثل حجم صخره ها ، گیاهان ، حیوانات و بسیاری چیزهای دیگر .
همان طور که سه شکل دایره ،مربع ومثلث به عنوان اشکال پایه برای سطح نام برده شدند ، دایره ،مکعب و هرم را نیز می توان به عنوان اجسام هندسی پایه نام برد. این سه نوع حجم به طور کاملاً منظم به ندرت در طبیعت دیده می شوند . اما به طور کلی همه ی حجم های طبیعت از ترکیب یا تغییر شکل این سه حجم پایه و هندسی به وجود می آیند .
ازچرخش یک مثلث به دور محور عمودی خودش حجمی به وجود می آید که به آن مخروط گفته میشود. از حرکت دورانی سطوح مربع و مستطیل شکل نیز استوانه ای حاصل می شود که دارای سه سطح تحتانی ،بالایی وجانبی است .از چرخش دایره نیز به دور محور قطری خودش حجم کره ساخته می شود.
نمایش حجم در فضا و روابط متقابل آن با فضای پیرامونش اصل مهم مجسمه سازی است. این روابط در نقش برجسته سازی که از یک سو با نقاشی و از سوی دیگر با معماری در ارتباط است اهمیتی به سزا دارد.
در معماری ایرانی انواع حجم های هندسی کاربرد دارد .بخشی از هنرنمایی نقاشان در طول تاریخ هنر برای واقع نمایی اجسام، شبیه سازی اشکال طبیعت به صورت سه بعدی بر
در معماری ایرانی انواع حجم های هندسی کاربرد دارد .بخشی از هنرنمایی نقاشان در طول تاریخ هنر برای واقع نمایی اجسام، شبیه سازی اشکال طبیعت به صورت سه بعدی بر سطح دو بعدی بوم نقاشی بوده است
تناسب
تناسب مفهومی ریاضی است که در هنر تجسمی بر رابطه ی مناسب میان اجزا ء با یک دیگر و با کل اثر دلالت دارد کاربرد تناسبات به دلیل ایجاد زیبایی بصری در هنر های تجسمی از اهمیتی ویژه برخوردار است . تقریبا″ همه ی آثار هنری بر اساس نوعی تناسب به وجود آمده اند . ازاین جهت تناسب یکی از اصول اولیه اثر هنری است که رابطه ی هماهنگ میان اجزاء آن را بیان می کند .
تناسب ، عبارت است از :رابطه نسبی و قیاسی بین اجزای مختلف و تمامی یک عنصر . تناسب گاهی از طریق کشف و شهود و بینش و زمانی از راه اعمال نسبت های ریاضی به وجود می آید . در آثار هنر های بصری ، نسبت های ریاضی ، در ایجاد تناسبات ، همان قدر زیبا و دارای ارزش است که نسبت های موجود در ساختمان اندام های طبیعت .
معمولا″ تشخیص تناسب و ایجاد روابط مناسب میان اجزاء یک اثر هنری ومیان اجزاء با کل اثر براساس تجربه مهارت و ذوق زیبایی شناختی هنرمند می باشد . مثل ایجاد تناسب میان رنگ ها و سایه ی رنگ های یک تابلو نقاشی . در آفرینش یک اثر هنری ، باید به مقدار نسبت های موجود بین عناصر بصری ، توجه ویژه ای چه مقدار فضا ، چه اندازه نور ، در کنار چه اندازه تاریکی و چه مقدار بافت زبر و خشن ، در برابر چه مقدار بافت نرم و لطیف قرار دارد
اندازه ی قسمت های مختلف بدن و تناسبات آن از دیر باز مورد توجه هنرمندان بوده است . آن ها همواره سعی کرده اند پیکره انسان را با زیباترین تناسبات طراحی کند .
استفاده از نسبت های ریاضی ، در ارائه تناسبات زیبا در یک کمپوزیسیون ، همواره مورد توجه هنرمندان مختلف در سراسر تاریخ بوده است . یکی از این نسبت های ریاضی قانون « نسبت های طلائی » است که اینک به بررسی آن می پردازیم .
نسبت های طلائی
معمولا″ تشخیص تناسب وایجاد روابط مناسب میان اجزاء یک اثرهنری ومیان اجزاء باکل اثر براساس تجربه ،مهارت وذوق زیبایی شناختی هنرمند می باشد .تناسب دراندازه ها ازقوانین خاصی پیروی می کند که به آن ها اصول وقواعد تقسیمات طلایی ویا تناسبات طلایی گفته می شود .
قانون «تقسیمات طلایی » درقرن سوم قبل از میلاد ، توسط اقلیدس فیلسوف وریاضیدان برجسته یونانی کشف شد .این قانون توسط هنرمندان یونانی وسپس هنرمندان دوره رنسانس درقرن پانزدهم وشانزدهم ایتالیا ،مورد استفاده قرارمی گرفت وبعداز آن نیز در آکادمی ها ومراکز آموزش هنر ،به عنوان قانون رسمی در مورد ایجاد تناسبات زیبا پذیرفته شد . از نخستین روزهای فلسفه یونان ، مردمان کوشیده اند ، که در هنر یک قانون هندسی پیدا کنند ، زیرا که اگر هنر( که آنرا با زیبایی یکی می دانند) همان هم آهنگی باشد ، وهم آهنگی هم از رعایت تناسبات حاصل شود ، منطقی به نظر می رسد که فرض کنیم این تناسبات ثابت اند . تناسب هندسی معروف به «تقسیم طلایی» ، قرن ها به عنوان یک همچو کلیدی برای اسرا ر هنر درنظر گرفته می شد وکاربرد آن نه تنها در هنر ، بلکه در طبیعت نیز چنان عمومیت دارد ، که گاهی حرمت مذهبی نسبت به آن معمول داشته اند .
x2-x-1=0 در ریاضی ریشه های معادله ی
یعنی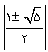
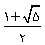
با بررسی های روان شناختی معلوم شده است مستطیل هایی با این قطع که گاه قطع وزیری نامیده می شوند زیبا تر از هر مستطیل دیگر در نظر جلوه می کند . دلیل این امر همان است که فرق یک چهره ی زیبا و زشت است . در یک انسان معمولی اندام های صورت از نظر چشم ، بینی ودهان وغیره مشخص است . آن چه چهره را زیبا جلوه می دهد تناسب بین آن ها است وجالب است که بدانید این تناسب مثلا″نسبت پیشا نی به باقیمانده طول صورت یا نسبت طول بینی به مجموع طول پیشا نی و فاصله ی بین بینی تا چانه در یک چهره زیبا همان عدد طلایی است.
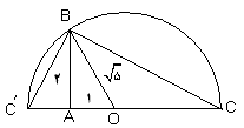
به طور کلی اگر سه نقطه روی یک خط مستقیم باشد نسبت قطعه ی بزرگ به قطعه ی کوچک برابر نسبت طول تمام پاره خط به طول قطعه ی بزرگ باشد می گوییم این سه نقطه روی این خط یک تقسیم طلایی به وجود آورده اند . (مانند شکل زیر )
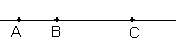
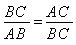
یونانی هایی که در بند زیبایی هنر وصنعت اسیر بودند این نسبت را از هزاران سال قبل
می شناختند ودر کارهای معماری ومجسمه سا زی خود به کار می بردند وآنرا تقسیم ملکوتی نیز می خوا ندند
از نظر هندسی تقسیم طلایی را می توان به کمک شکل زیر به دست آورد :
که در این جا 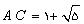
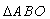
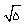
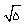
و مرکز O ضلع OA را در نقاط C و' C قطع می کند
. و لذ ا
۱،۱،۲،۳،۵،۸ ...
که جمله ی عمومی این دنبا له :
در این دنبا له نسبت هر جمله به جمله ی ماقبل خود هر چه تعداد جملات زیاد می شود به عدد طلایی نزدیک میشود.
می توان به سادگی ثابت کرد که وقتی 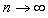
دنباله ی فیبو ناتچی یکی ا ز زیبا یی های ریاضی است . در خواص آن مطالعات زیادی شده است و مجله ای تحت عنوان خواص دنباله ی فیبو ناتچی هر سه ماه یک بار چاپ می شود که یکی از عجا یب ریاضی است . یک بر رسی ا نجام شده ی دیگر دررابطه با این نسبت نشان می دهد که دراسباب های خانگی و مبل ها ی کاخ لو یی شانزدهم این نسبت ملاحظه میشود که در حقیقت یکی از زیبا ترین و مناسب ترین مبلمان موجود است .
در موسیقی نسبت های زمانی آهنگ em it Last Theاثر مشهور لویی ا رمسترانگ موسیقی دان و جازیست مشهور سیاهپوست آمریکا یی این نسبت رعایت شده و ا ین اثر ماندگار را به جا گذاشته است . آهنگسازانی که کمی با ریاضی آشنا هستند معتقدند در زیبا ترین قطعا ت موسیقی کلاسیک آن ها ندانسته به ا ین نسبت زمانی برخورد کرده اند .
در نقا شی های کوبیسم به خصوص در تابلوی مشهور پیکاسو که حدود ۲۷سال قبل به قیمت چهل میلیون دلار در حراج به فروش رفت بارها این نسبت تکرا ر شده است .
در عصرما نیز ، در کلیه ی رشته های هنر های تجسمی ، مورد استفاده هنرمندان قراردارد ، در معماری برای ایجاد فضا های زیست ، طراحی پنجره و نرده ها ، در گرافیگ در بخش « لی آت » روز نامه و مجله و کتاب و در منظره سازی نسبت فضای بالا ی خط افق به نسبت فضا ی زمین و نیز تقسیمات عمودی موجود در تابلو ، همگی تابع قانون تقسیمات طلایی هستند .
ساختمان اهرام سه گانه مصر و تناسبات موجود در معماری کلیساهای به سبک « گوتیک » نیز با استفاده از همین قانون انجام شده است .
هندسه در معماری
آثار معماری گذشته به ویژه آنهایی که بیانگر تمدنهای عظیم بشری هستند، نشان دهنده ی به کارگیری عمیق و وسیع هندسه در طراحی معماری بوده اند واساساً در همه این ادوار،طرح معماری بدون پوشش هندسی نشانه عدم خلاقیت به شمار می رفته واین امر تا بدان جا پیش رفته است که بناهای عظیم و ماندگار دوران گذشته خود را مقید به هندسه مطلق نموده و به خاطر رعایت جنبه های نظم در حد اعلای آن، حتی بسیاری موارد دیگر معماری را فدا نموده اند.
همچنین توجه به این نکته نیز حایز اهمیت است که ابزار مورد استفاده برای معماری (از قبیل پرگار،گونیا،انواع درافتینگ،نرم افزارهای نقشه کشی و ...)حاوی بخش عمدهای از قضایا واحکام هندسه اقلیدسی و همچنین حاوی بعضی فنون تاریخی استفاده از هندسه در معماری هستند و تولیدکنندگان این ابزارها بر روی نکات عمده ی این فنون تاکید کرده اند.
عالیترین بعد، هندسه به کارگیری آن در ترکیب شکلها وحجمهاست.تنها در این است که می توان ساختار هندسی طرحهای معماری را از هم باز شناخت ومیزان خلاقیت وتسلط طراح را دریافت.
علم هندسه مثل همه علوم دیگر از مشاهده وتجربه ناشی شده وارتباط جدی با احتیاجات اقتصادی بشر دارد کلمه هندسه در زبانهای اروپایی، ریشه یونانی دارد وبه معنای مساحی (اندازه گیری زمین) است. به هر تقدیر آغاز دانش هندسه را به تجارب مساحی ومعماری نسبت داده اندو اولین قدمهای آن در ترسیم روی زمین صورت گرفته است.
اولین آثار ترسیمات و احداثات منظم به دوران نوسنگی، یعنی در حقیقت هنگامی که اولین آثار تقسیم کار ظاهر می شود و مشاغل مساحی ومعماری پدید می آید، تعلق دارد.
تقارن
طبیعت عنصر تقارن را به عنوان نشانه زیبایی به هنرمند تلقین می کند و افلاطون ، تقارن مظهر و معیار زیبایی می دانست.
تقارن را در بسیاری از پدیده های طبیعی مانند حیوانات ، گیاهان و اندام انسان در حالت ایستاده از طرف پشت و جلو و بسیاری از اشیاء ساخته دست بشر مانند بعضی از معماری های کلاسیک مثل معماری دوران گوتیک ، روکوکو ، معماری اسلامی مشاهده کرد.درهنرهای اسلامی ،نقاشان قدیمی ، با الهام از این مواهب خداوندی ، نقش ونگارهای زیبایی ابداع کرده اند که گلهای قالی و کاشی و سایر هنرهای دستی ، نمونه خوبی از ذوق آنها است .
نتیجه گیری
آدمی ، از همان روزهایی که می شنود ،می بیند و درک می کند ، ازموسیقی و نقاشی و شعر لذت می برد و چه به صورت لالایی مادر باشد یا آهنگ گوش نواز چایکووسکی، چه بیتی عامیانه و کوچه باغی باشد با سرودی از لسان الغیب ، چه هنر مندی در قالی های دست باف باشد و چه ظرافت ها و رنگهای چشم نواز بهزاد و کمال الملک همه جا انسان را به سوی خود می کشاند و غرق در آرامش و لذت می کند . ولی همه اینها ، یک شرط اساسی دارد و آن این است که آفریننده آنها استادی باشد که از شیوه درست ومنطقی برای بیان موضوع استفاده کرده باشد .
"و ریاضی بهترین شیوه برای بیان یک مطلب منطقی می باشد و ریاضیات کلید طلایی برای زیبایی شناسی است ."
در واقع تمامی عرصه ریاضییات ، سرشار از زیبایی و هنر است. زیبایی ریاضیات را می توان در شیوه بیان موضوع ، در طرز نوشتن و ارائه آن ، در استدلالهای منطقی آن ، در رابطه آن با زندگی و واقعیت ، در سرگذشت پیدایش و تکامل آن و در خود موضوع ریاضی مشاهده کرد.
بنابراین ریاضی و هنر دو علم جدایی ناپذیرند .
منابع:
بررسی کاربرد هندسه در معماری / مؤلف : بهزاد مولوی .-تهران مرکز تحقیقات ساختمان و مسکن
آموزش هنر / مؤلف: محمد مهدی هراتی . –شرکت چاپ و نشر کتابهای درسی.
مبانی هنرهای تجسمی / مؤلف: عبدالمجید حسینی راد .-شرکت چاپ و نشر کتابهای درسی .
مبانی هنر های تجسمی / مؤلف : غلامحسین نامی . –تهران ، انتشارات توس


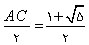
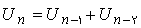

با درود و سلام خدمت شما دوست عزیز
سایت بسیار قشنگ،جذاب وپرمحتوایی دارید.من admin هستم. و فرومی آموزشی،علمی و تخصصی برای تمام ایرانیان راه اندازی کردم. خوشحال می شوم از تخصص و مهارت شما به عنوان مدیری لایق و کاردان بهره مند شوم.درصورت علاقه بازدیدی بفرمایید.
www.p30stars.net
موفق باشید.منتظر حضور سبز شما هستم.
از مقاله شما بی نهایت متشکرم واقعا؛ استفاده کردم
با سلام
احسنت .
واقعا مقاله شما در خور تحسین و تمجید است
سلام. کارتان بسیار ارزشمند است.از مقاله تان (هرچند در بعضی از بخش ها تکراری است ) بسیار سود بردم.و در کلاس های آینده ام استفاده خواهم کرد....ممنونم.در پناه حق